Pipeline Stress Analysis

Hoop Stress & Barlow's Formula

Hoop stress is the primary design consideration for pressure containment in pipelines and process piping. This guide covers Barlow's formula, ASME B31.8/B31.3 design requirements, and code compliance.

Launch Calculator Barlow's Formula

Stress Relationship

σh = 2 × σL

Hoop stress is 2× longitudinal stress—always the governing design limit.

Design Factors

0.40 – 0.72

Class 1 = 72% SMYS, Class 4 = 40% SMYS per 49 CFR 192.111.

Thin-Wall Limit

D/t > 20

Barlow's formula accurate when diameter-to-thickness ratio exceeds 20.

Contents

Quick Start

Try the Calculator

Calculate hoop stress, MAOP, and verify code compliance.

Open Calculator →

1. Cylinder Stress Theory

When a pipe is pressurized internally, stress develops in the pipe wall in three directions: circumferential (hoop), longitudinal (axial), and radial. For thin-walled pipes, hoop stress dominates and is the basis for pressure design.

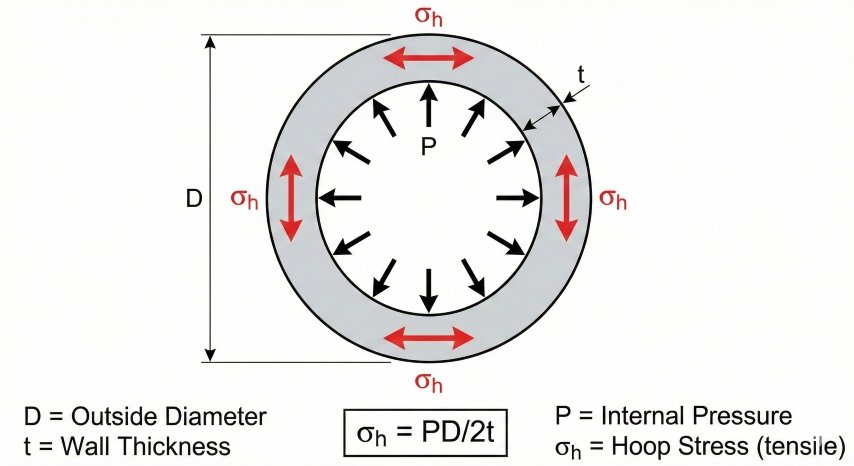
Cross-section of pressurized pipe showing internal pressure P acting radially outward and hoop stress σh acting circumferentially as tensile forces in the pipe wall
Hoop stress in pressurized pipe: Internal pressure creates circumferential tensile stress in the wall.

Thin-Wall Assumption

Barlow's formula assumes uniform stress distribution through the wall thickness. This is valid when:

  • D/t > 20: Stress varies less than 5% through wall
  • D/t > 10: Acceptable for design (error < 10%)
  • D/t < 10: Use Lamé equations for thick-wall analysis
Why hoop stress governs: For a closed cylinder under internal pressure, hoop stress is exactly twice the longitudinal stress. Pipeline design focuses on hoop stress because it's always the maximum principal stress.

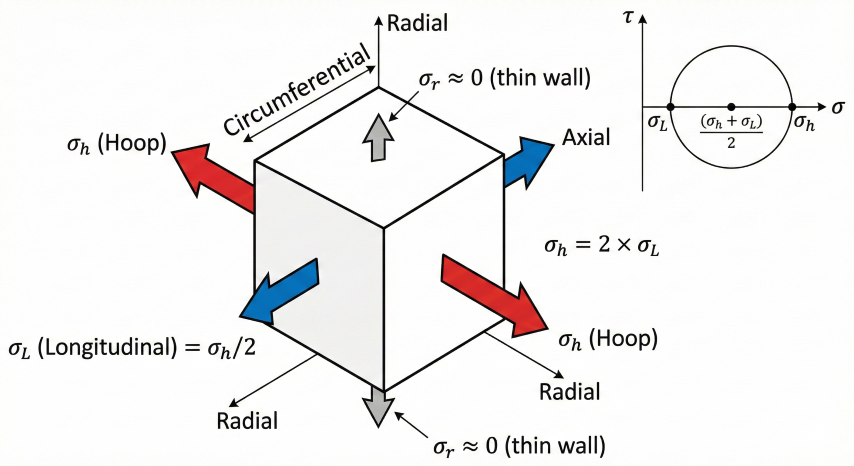
Principal Stresses in Pressurized Cylinders

Stress Component Formula (Thin-Wall) Ratio to σh
Hoop (circumferential) σh = PD / 2t 1.00
Longitudinal (axial) σL = PD / 4t 0.50
Radial σr ≈ −P (ID) to 0 (OD) ≈ 0 (thin-wall)
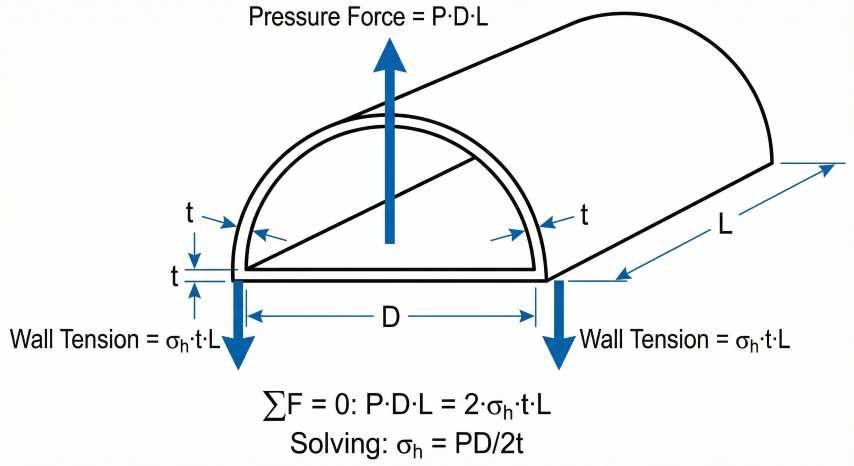
Free body diagram of half-cylinder section showing pressure force P×D×L balanced by wall tension forces σh×t×L on both sides, deriving Barlow's formula
Free body diagram derivation: Pressure force on projected area equals wall tension forces, yielding σh = PD/2t.

2. Barlow's Formula

Peter Barlow published this formula in 1836 for calculating stress in cylindrical pressure vessels. It remains the fundamental equation for pipeline design.

Barlow's Formula (49 CFR 192.105): S = (P × D) / (2 × t) Where: • S = Hoop stress (psi) • P = Internal pressure (psig) • D = Outside diameter (inches) • t = Nominal wall thickness (inches)

Rearranged Forms

Solve For Formula Application
Wall thickness t = PD / (2S) Minimum wall for given pressure
Pressure (MAOP) P = 2St / D Maximum allowable pressure
Stress S = PD / 2t Verify existing pipe

OD vs. Mean Diameter

The regulatory formula (49 CFR 192.105) uses outside diameter, which yields a conservative (higher) stress. For more accurate stress analysis:

Mean Diameter Method (More Accurate): σ_h = P × D_mean / (2 × t) Where D_mean = D - t Difference from OD method ≈ (t/D) × 100% For typical pipelines: 2-4% lower stress

Example Calculation

Given: 16" OD × 0.375" wall, 1000 psig, X52 pipe

S = (1000 × 16) / (2 × 0.375)
S = 16,000 / 0.75
S = 21,333 psi (41% of 52,000 SMYS)

3. ASME B31.8 Design Factors

Pipeline codes limit allowable stress to a fraction of the pipe's Specified Minimum Yield Strength (SMYS). The complete design equation includes multiple factors:

Design Pressure Formula (49 CFR 192.105): P = (2 × S × t × F × E × T) / D Where: • S = SMYS (psi) • F = Design factor (0.40 – 0.72) • E = Longitudinal joint factor (0.60 – 1.00) • T = Temperature derating factor (≤ 1.00)

Design Factor (F) by Location Class

Class F %SMYS Description
1 0.72 72% Rural (≤10 buildings/mile)
2 0.60 60% Fringe (11–46 buildings)
3 0.50 50% Suburban (≥46 buildings)
4 0.40 40% Urban (multi-story prevalent)

Joint Factor (E) per ASME B31.8 Table 841.1.7-1

Pipe Type E Factor
Seamless 1.00
ERW/EFW (post-1970) 1.00
ERW (1960–1970) 0.85
ERW/Flash Weld (pre-1960) 0.80
Spiral Weld 0.80–1.00
Furnace Butt Weld 0.60

Temperature Derating (T) per Table 841.1.8-1

Temperature (°F) T Factor
≤ 250 1.000
300 0.967
350 0.933
400 0.900
450 0.867

Common SMYS Values (API 5L)

Grade SMYS (psi) SMYS (MPa)
B 35,000 245
X42 42,000 290
X52 52,000 360
X60 60,000 415
X65 65,000 450
X70 70,000 485
X80 80,000 555

4. ASME B31.3 Process Piping

ASME B31.3 governs process piping in refineries, chemical plants, and gas processing facilities. Unlike B31.8's location-based design factors, B31.3 uses allowable stress values derived from material properties with safety factors applied.

Wall Thickness Formula

B31.3 uses a modified Barlow's formula that accounts for internal pressure's contribution to stress:

Required Wall Thickness (ASME B31.3 §304.1.2): t = PD / (2(SE + PY)) Where: • t = Minimum required thickness (inches) • P = Internal design pressure (psig) • D = Outside diameter (inches) • S = Allowable stress from Table A-1 (psi) • E = Weld joint quality factor • Y = Coefficient from Table 304.1.1

Y Coefficient (Table 304.1.1)

The Y coefficient accounts for stress redistribution in the pipe wall under pressure. It varies with temperature and material type:

Material ≤900°F 950°F 1000°F ≥1050°F
Ferritic steels 0.4 0.5 0.7 0.7
Austenitic steels 0.4 0.4 0.4 0.4
Nickel alloys 0.4 0.4 0.4 0.4

Simplified: For temperatures ≤900°F and D/t > 6, Y = 0.4 is commonly used.

Allowable Stress (S)

B31.3 allowable stress is the lower of:

  • SMYS / 3.0 (yield-based)
  • SMTS / 3.0 (tensile-based)
  • Stress-rupture at temperature (creep range)
Key Difference from B31.8: B31.8 allows up to 72% SMYS (F = 0.72), while B31.3's SMYS/3 equates to only 33% SMYS. B31.3 is more conservative because process piping often has more complex loading, thermal cycles, and corrosive environments.

Weld Joint Quality Factor (E)

Per B31.3 Table A-1B:

Joint Type E Factor
Seamless pipe 1.00
ERW (ASTM A53 Type E) 1.00
Furnace butt weld (ASTM A53 Type F) 0.60
Electric fusion weld (double) 1.00
Electric fusion weld (single) 0.80
API 5L (ERW, SMLS, DSAW) 1.00

MAWP Calculation

Maximum Allowable Working Pressure for existing pipe:

MAWP (B31.3): P = (2 × S × E × t) / (D - 2 × Y × t) For thick-wall pipe (D/t < 6): P = (2 × S × E × t) / (D - 2 × t) Hydrostatic test = 1.5 × Design Pressure

Example: B31.3 vs B31.8

Given: 8" Sch 40 (OD=8.625", t=0.322"), 52,000 psi SMYS, 100°F

B31.8 (Class 1):
P = 2 × 52,000 × 0.322 × 0.72 / 8.625
P = 2,794 psig

B31.3:
S = 52,000 / 3 = 17,333 psi
P = 2 × 17,333 × 1.0 × 0.322 / (8.625 - 2×0.4×0.322)
P = 11,162 / 8.367 = 1,334 psig

B31.3 yields ~48% of B31.8 allowable pressure due to more conservative safety factors.

5. Location Classification

Location class determines the design factor and is based on building density along the pipeline corridor. Per 49 CFR 192.5:

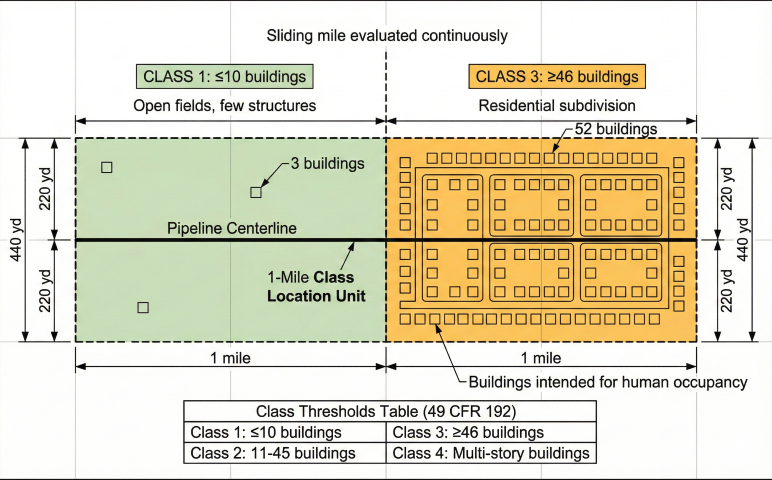
Aerial view diagram showing pipeline location class determination method with 1-mile by 440-yard sliding window, comparing Class 1 rural (≤10 buildings) versus Class 3 suburban (≥46 buildings) examples
Location class determination: Count buildings within 220 yards of pipeline over 1-mile sliding window.

Class Definitions

  • Class 1: ≤10 buildings intended for human occupancy within the 1-mile × 440-yard sliding rectangle
  • Class 2: 11–46 buildings, or an area where development is likely
  • Class 3: ≥46 buildings, or within 100 yards of a building with 20+ occupants (schools, churches, hospitals)
  • Class 4: Areas where 4+ story buildings are prevalent
Class Changes: Pipeline operators must monitor for development. If building count increases beyond class limits, the pipeline may require uprating or replacement to meet the lower design factor.

6. Design Applications

New Pipeline Design

Select wall thickness for design pressure and location class:

Problem: Select wall for 24" pipeline, 1200 psig MAOP, Class 1, X65 pipe

Given: D = 24", P = 1200 psig, S = 65,000 psi, F = 0.72, E = 1.0, T = 1.0

t = PD / (2 × S × F × E × T)
t = (1200 × 24) / (2 × 65,000 × 0.72 × 1.0 × 1.0)
t = 28,800 / 93,600
t = 0.308" → Select 0.344" (STD) or 0.375"

Manufacturing Tolerance

API 5L PSL2 allows negative tolerance on wall thickness:

  • t ≤ 0.197" (5 mm): −12.5%
  • t > 0.197": −10% (min 0.5 mm)

For stress verification of existing pipe, use minimum wall (nominal × 0.875 or 0.90).

Von Mises Equivalent Stress

For combined stress analysis (ductile materials):

Von Mises Stress (Biaxial): σ_vm = √(σ_h² - σ_h×σ_L + σ_L²) For internal pressure only (σ_L = σ_h/2): σ_vm = √(0.75 × σ_h²) = 0.866 × σ_h Yield occurs when σ_vm ≥ SMYS
3D stress element from pipe wall showing hoop stress σh acting circumferentially, longitudinal stress σL acting axially with σh = 2×σL relationship, and Mohr's circle inset
Stress state in pipe wall: Hoop stress is twice longitudinal stress, making it the governing design criterion.

7. Code Requirements

Applicable Codes & Regulations

Code Application Jurisdiction
49 CFR Part 192 Gas transmission & distribution DOT/PHMSA (Federal)
49 CFR Part 195 Hazardous liquids DOT/PHMSA (Federal)
ASME B31.8 Gas transmission design Industry (referenced)
ASME B31.3 Process piping (plants) Industry standard
ASME B31.4 Liquid petroleum Industry (referenced)
API 5L Line pipe specification Industry standard

Regulatory Hierarchy: 49 CFR 192/195 are federal regulations (mandatory). ASME B31.8/B31.4 are industry codes referenced by regulations. When conflicts exist, federal regulations take precedence.

Hydrostatic Testing (49 CFR 192.505)

Location Class Minimum Test Pressure Duration
Class 1 1.25 × MAOP 8 hours
Class 2 1.25 × MAOP 8 hours
Class 3 1.40 × MAOP 8 hours
Class 4 1.40 × MAOP 8 hours

Industry Practice: 1.5× MAOP is common for new construction to establish MAOP margin.

Key Design Requirements

  • Maximum stress: 72% SMYS for Class 1 gas transmission
  • Manufacturing tolerance: Account for −12.5% wall per API 5L
  • Corrosion allowance: Add to minimum calculated thickness
  • Pressure surge: May require additional wall for water hammer

References

  • 49 CFR Part 192 – Transportation of Natural Gas by Pipeline (DOT/PHMSA)
  • 49 CFR Part 195 – Transportation of Hazardous Liquids by Pipeline
  • ASME B31.8-2022 – Gas Transmission and Distribution Piping Systems
  • ASME B31.3-2022 – Process Piping
  • ASME B31.4-2022 – Pipeline Transportation Systems for Liquids
  • API 5L (46th Edition) – Specification for Line Pipe
  • ASME B31G – Manual for Determining Remaining Strength of Corroded Pipelines

Ready to use the calculator?

→ Launch Calculator