Pipeline Basics

Pipe Flow Area Calculations

Calculate internal cross-sectional area for velocity determination, flow rate analysis, and hydraulic calculations using inside diameter, wall thickness, and standard pipe schedules per ASME B36.10M.

Launch Calculator Velocity relationships

Area formula

A = π × d² / 4

Flow area from inside diameter: A (in²) = 0.7854 × d² where d = ID in inches.

Typical values

12" Std: 113.1 in²

12" NPS Standard pipe (OD=12.75", WT=0.375"): ID = 12.00", flow area = 113.1 in².

Velocity relation

V = Q / A

Flow velocity: V (ft/s) = Q (ft³/s) / A (ft²). Critical for erosion and hydraulic analysis.

Contents

Quick start

Try the calculator

Calculate flow area from pipe size, or determine velocity and flow rate for your pipeline.

Open calculator →

1. Area Calculation

Flow area is the internal cross-sectional area available for fluid flow. It's fundamental to velocity calculations, pressure drop analysis, and equipment sizing.

Basic Formula

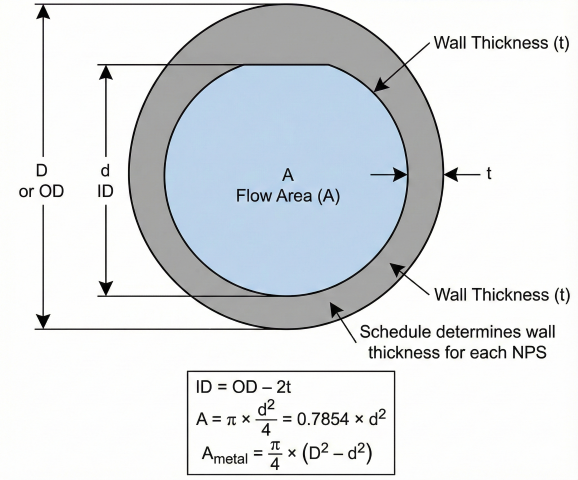
Pipe cross-section diagram showing outer diameter (OD), inner diameter (ID), wall thickness (t), and shaded flow area (A) with key formulas for ID = OD - 2t and A = π × d²/4
Pipe cross-section showing dimensional relationships between OD, ID, wall thickness, and flow area
Internal flow area: A = π × d² / 4 Practical forms: A (in²) = 0.7854 × d² A (ft²) = 0.005454 × d² [d in inches] A (ft²) = 0.7854 × d² [d in feet] Where d = inside diameter

Inside Diameter

d = D - 2t Where: d = Inside diameter D = Outside diameter (per ASME B36.10M) t = Wall thickness (nominal) Manufacturing tolerance (API 5L / ASTM A530): Wall thickness: ±12.5% of nominal t_min = t × 0.875 (thinnest allowable) t_max = t × 1.125 (thickest allowable)
Design implication: Minimum wall gives maximum ID and maximum flow area. For conservative pressure drop calculations, use maximum area (minimum wall). For hoop stress calculations, use minimum wall.

Metal Area (Pipe Wall)

Cross-sectional metal area: A_metal = π/4 × (D² - d²) A_metal = π × (D - t) × t Used for: weight calculation, stress analysis

Ovality Effect (Out-of-Roundness)

Per API 5L Table 10: OD < 8.625": Max ovality = 1.0% OD 8.625" to 12.75": Max ovality = 1.0% OD ≥ 12.75": Max ovality = 1.5% Area reduction formula: A_oval ≈ A_circular × (1 - ε²) Where ε = ovality (decimal) Example: 1.5% ovality A_oval = A × (1 - 0.015²) = A × 0.999775 Area reduction = 0.0225% (negligible)
Practical note: Ovality has a second-order (squared) effect on area. Even 2% ovality only reduces area by 0.04%. This is typically negligible but included in precise hydraulic calculations.

2. Velocity Relationships

Flow area connects volumetric flow rate to fluid velocity through the continuity equation.

Continuity Equation

Q = A × v Rearranged: v = Q / A (velocity from flow rate) A = Q / v (required area for target velocity) Q = A × v (flow rate from velocity)

Practical Velocity Formulas

Liquid velocity (ft/s): v = 0.4085 × Q / d² Where Q = flow rate (gpm), d = ID (inches) Gas velocity (ft/s): v = 60 × Q_acfm / A_ft² Or at standard conditions: v = 0.4615 × Q_scfm × (P_std/P) × (T/T_std) × Z / d² Gas velocity (ft/s) simplified: v = Q_MMSCFD × 6.316 × T × Z / (P × d²) Where T in °R, P in psia, d in inches

Recommended Velocities

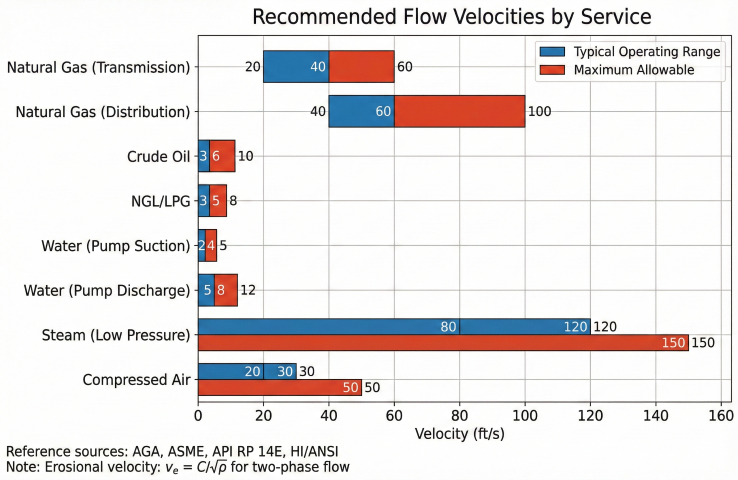
Horizontal bar chart showing recommended flow velocities by service type including natural gas transmission and distribution, crude oil, NGL/LPG, water pump suction and discharge, steam, and compressed air with typical operating range and maximum allowable values
Recommended flow velocities by service (Reference: AGA, ASME, API RP 14E, HI/ANSI)
Service Typical (ft/s) Maximum (ft/s) Reference
Natural gas (transmission) 20–40 60 AGA, ASME B31.8
Natural gas (distribution) 40–60 100 ASME B31.8
Crude oil 3–6 10 API RP 14E
NGL/LPG 3–5 8 GPSA
Water (pump suction) 2–4 5 HI/ANSI
Water (pump discharge) 5–8 12 HI/ANSI
Steam (low pressure) 80–120 150 ASME B31.1
Compressed air 20–30 50 CAGI
API RP 14E erosional velocity: For two-phase flow, v_e = C / √ρ_m where C = 100–150 (conservative to less conservative) and ρ_m = mixture density (lb/ft³). This limits velocity to prevent erosion-corrosion.

3. Reference Tables

Standard Pipe Flow Areas

NPS OD (in) Schedule Wall (in) ID (in) Area (in²) Area (ft²)
2" 2.375 40 0.154 2.067 3.356 0.0233
4" 4.500 40 0.237 4.026 12.73 0.0884
6" 6.625 40 0.280 6.065 28.89 0.2006
8" 8.625 40 0.322 7.981 50.03 0.3474
10" 10.750 40 0.365 10.020 78.85 0.5476
12" 12.750 Std 0.375 12.000 113.1 0.7854
16" 16.000 Std 0.375 15.250 182.7 1.269
20" 20.000 Std 0.375 19.250 291.0 2.021
24" 24.000 Std 0.375 23.250 424.6 2.948
30" 30.000 Std 0.375 29.250 672.0 4.666
36" 36.000 Std 0.375 35.250 976.0 6.778

Area Ratios

Area ratio between pipe sizes: A₂/A₁ = (d₂/d₁)² Examples: 12" to 8": (12/8)² = 2.25× area increase Velocity decreases by same ratio: v₂ = v₁ × (d₁/d₂)²

4. Hydraulic Diameter

For non-circular cross-sections or partially filled pipes, hydraulic diameter relates flow area to wetted perimeter for use in friction factor correlations.

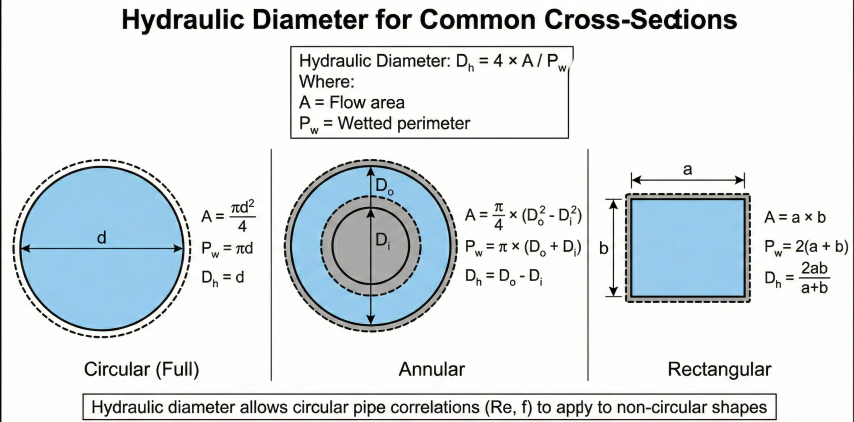
Hydraulic diameter diagram comparing circular, annular, and rectangular cross-sections with formulas for flow area, wetted perimeter, and hydraulic diameter Dh = 4A/Pw for each geometry
Hydraulic diameter for common cross-sections: D_h = 4A/P_w allows circular pipe correlations to apply to non-circular shapes

Definition

Hydraulic diameter: D_h = 4 × A / P_w Where: A = Flow area P_w = Wetted perimeter For circular pipe (full flow): D_h = 4 × (πd²/4) / (πd) = d For annulus (pipe in pipe): D_h = D_o - D_i (outer ID minus inner OD)

Common Cross-Sections

Shape Hydraulic Diameter
Circular (full) D_h = d
Circular (half full) D_h = d
Annulus D_h = D_outer - D_inner
Square (side a) D_h = a
Rectangle (a × b) D_h = 2ab/(a+b)
Equilateral triangle D_h = a/√3

Partially Filled Pipe

Flow at depth h in horizontal pipe: A = r² × [arccos((r-h)/r) - ((r-h)/r) × √(1-((r-h)/r)²)] P_w = 2r × arccos((r-h)/r) D_h = 4A / P_w At 50% full: D_h = d (same as full pipe) At 80% full: D_h ≈ 1.22d (higher than full!)

5. Applications

Reynolds Number

Re = ρ × v × D_h / μ = v × D_h / ν Using practical units: Re = 7742 × Q × SG / (d × μ) Where: Q = flow (gpm) d = ID (inches) μ = viscosity (cP) SG = specific gravity

Line Sizing Example

Problem: Size a water line for 500 gpm at max 8 ft/s

Required area:
v = 0.4085 × Q / d²
8 = 0.4085 × 500 / d²
d² = 204.25 / 8 = 25.5
d = 5.05 inches minimum

Select 6" Sch 40:
ID = 6.065 in
v = 0.4085 × 500 / 6.065² = 5.55 ft/s ✓

Orifice and Restriction Areas

Beta ratio (orifice sizing): β = d_orifice / d_pipe Area ratio: A_orifice / A_pipe = β² Typical ranges: - Orifice plates: β = 0.2–0.75 - Control valves: sized for Cv at design flow - Restrictions: pressure drop ∝ 1/A²

Common Uses

  • Line sizing: Select pipe diameter for target velocity
  • Pump selection: Calculate suction/discharge velocities
  • Pressure drop: Velocity head = v²/2g
  • Flow measurement: Orifice and venturi sizing
  • Heat transfer: Convection coefficient correlations
  • Erosion analysis: Check against erosional velocity limits

References

  • ASME B36.10M – Welded and Seamless Wrought Steel Pipe (dimensions)
  • API 5L – Specification for Line Pipe (tolerances, Table 10 ovality)
  • ASTM A530 – General Requirements for Carbon Steel Pipe (tolerances)
  • ASME B31.8 – Gas Transmission and Distribution Piping Systems
  • API RP 14E – Design and Installation of Offshore Production Piping (erosional velocity)
  • Crane TP-410 – Flow of Fluids Through Valves, Fittings, and Pipe
  • GPSA

Ready to use the calculator?

→ Launch Calculator