1. Why Average Pressure?
Gas flow equations require fluid properties (density, viscosity, compressibility factor Z) evaluated at a representative pressure. Since pressure varies along a pipeline due to friction losses, we need a single "average" value that, when used in flow equations, gives the correct result.
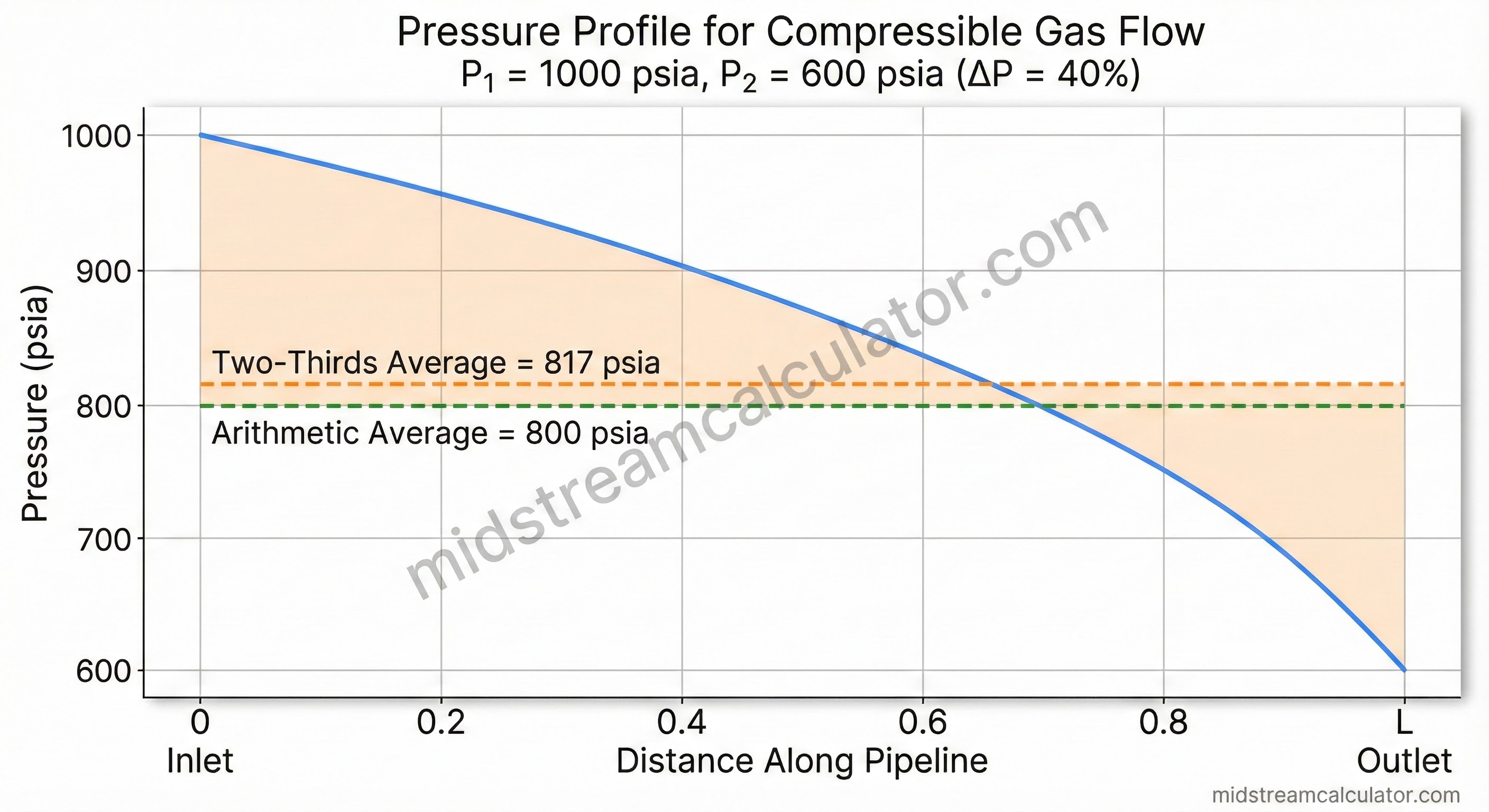
For compressible flow, pressure does not decrease linearly. Gas density decreases as pressure drops, causing velocity to increase. This non-linear behavior means the simple arithmetic average underestimates the effective average pressure.
2. Calculation Methods
Arithmetic Average
The simplest approach—just the midpoint between inlet and outlet pressures.
Two-Thirds Average (GPSA Method)
The industry-standard method for compressible gas flow, derived from integrating the pressure-flow relationship.
3. Mathematical Derivation
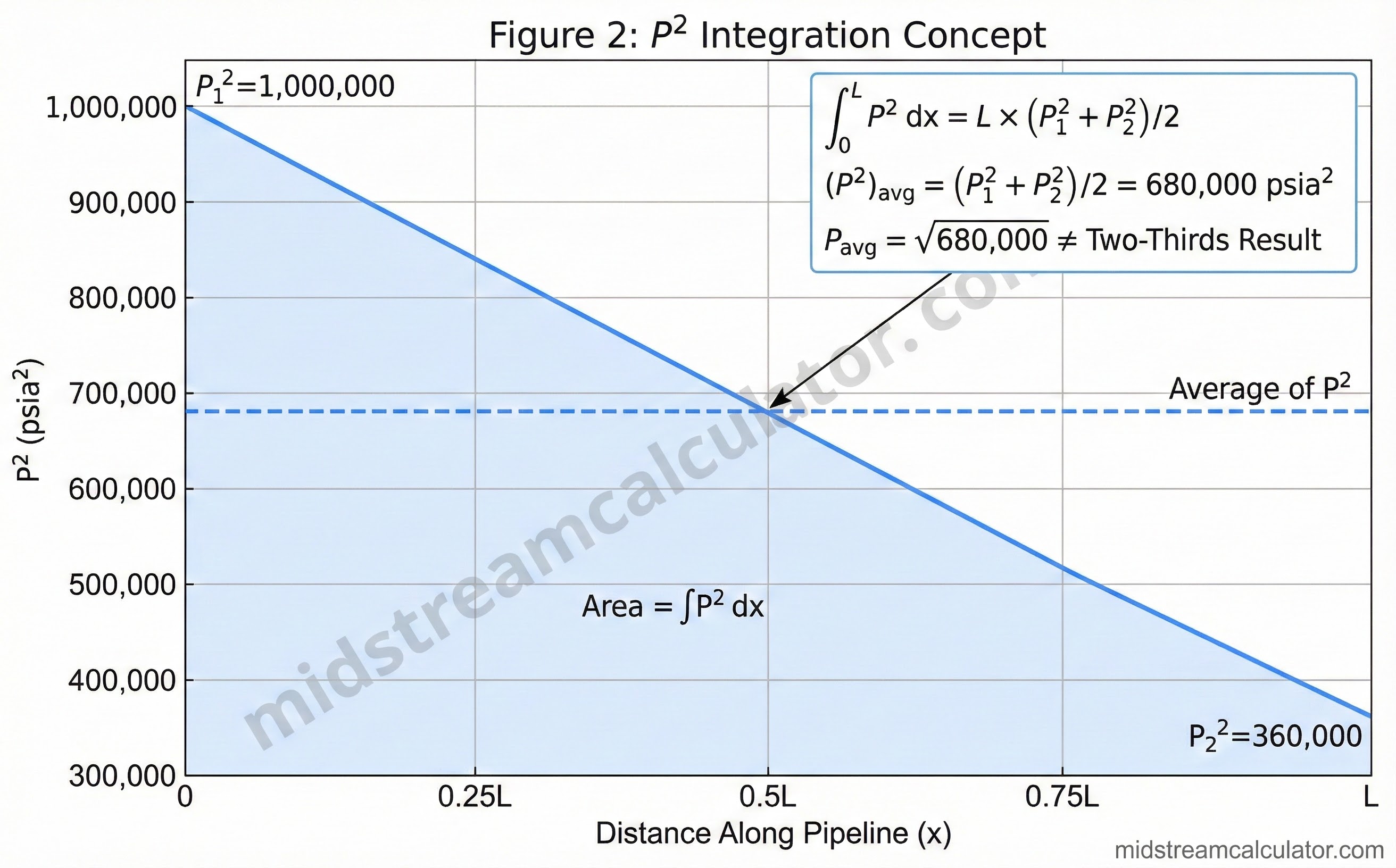
The two-thirds formula comes from the general flow equation for compressible flow, where flow rate Q is proportional to √(P₁² - P₂²).
4. Method Comparison
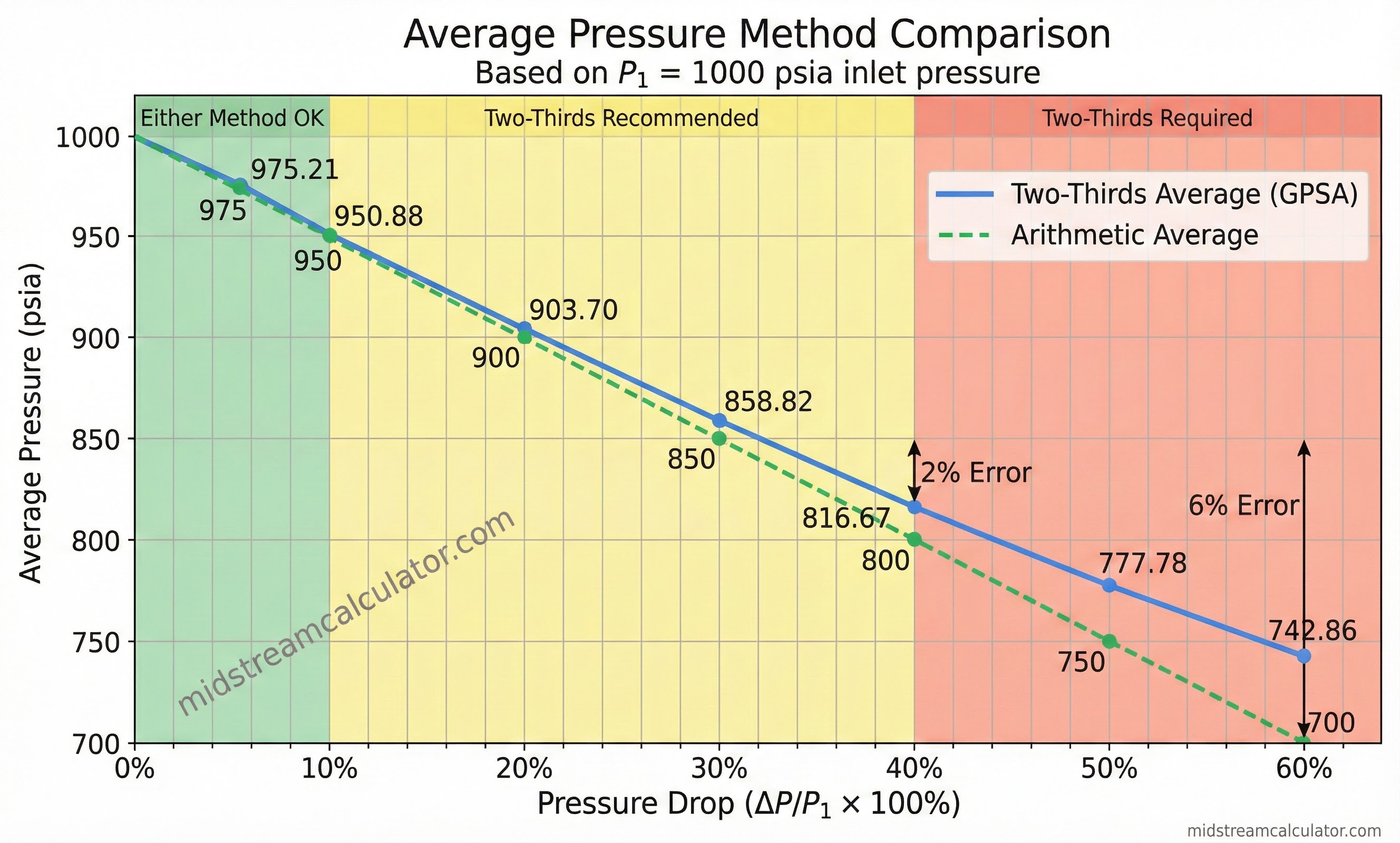
The table below shows how the two methods compare across different pressure drop scenarios.
| P₁ (psia) | P₂ (psia) | ΔP (%) | Arithmetic | Two-Thirds | Difference |
|---|---|---|---|---|---|
| 1000 | 950 | 5% | 975.00 | 975.21 | 0.02% |
| 1000 | 900 | 10% | 950.00 | 950.88 | 0.09% |
| 1000 | 800 | 20% | 900.00 | 903.70 | 0.41% |
| 1000 | 700 | 30% | 850.00 | 858.82 | 1.04% |
| 1000 | 600 | 40% | 800.00 | 816.67 | 2.08% |
| 1000 | 500 | 50% | 750.00 | 777.78 | 3.70% |
| 1000 | 400 | 60% | 700.00 | 742.86 | 6.12% |
• ΔP < 10%: Either method acceptable (difference < 0.1%)
• ΔP 10-40%: Two-thirds recommended for accuracy
• ΔP > 40%: Two-thirds required; arithmetic gives significant error
5. Atmospheric Pressure
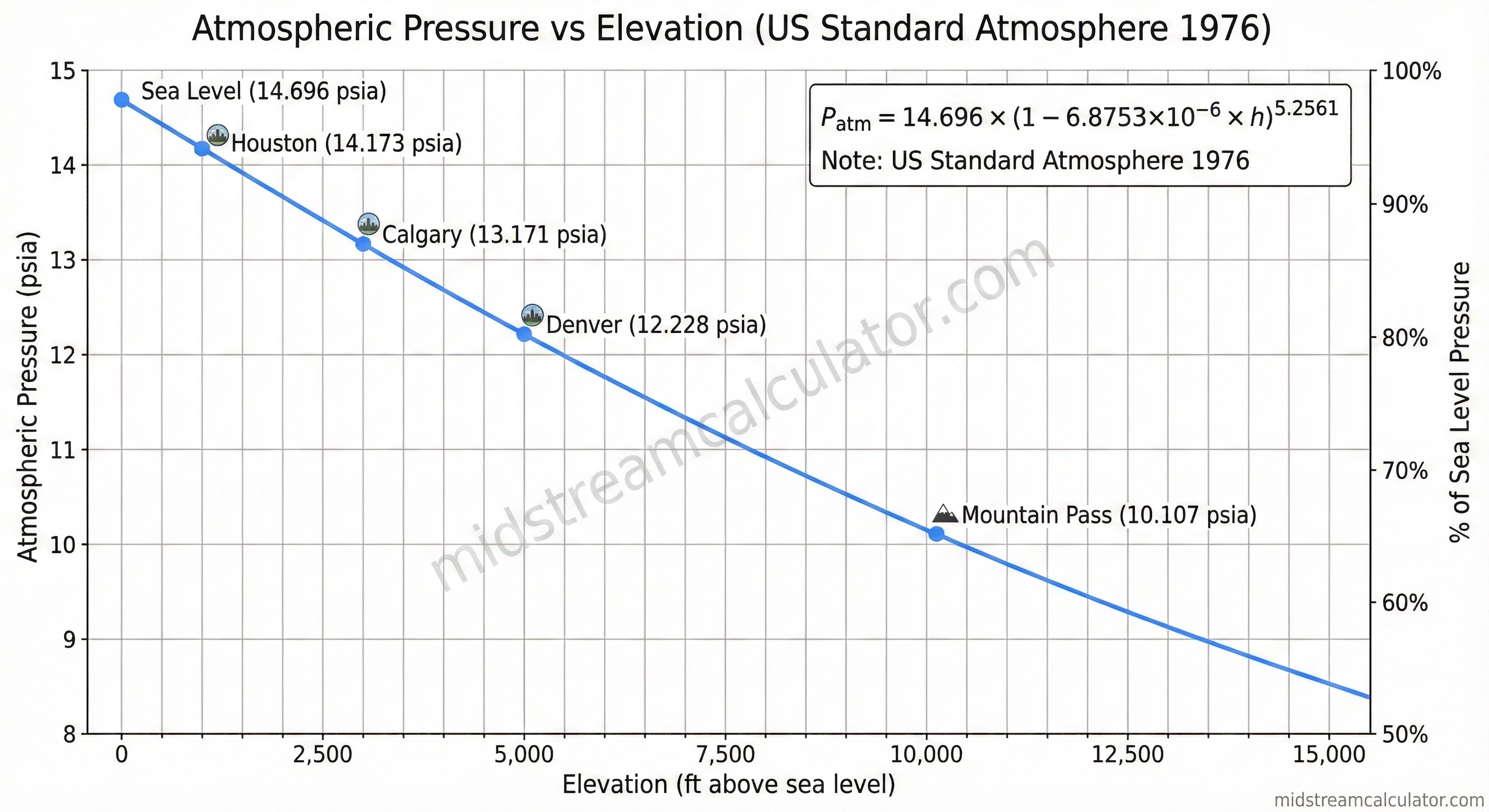
Gauge pressure must be converted to absolute pressure before applying average pressure formulas. At high elevations, atmospheric pressure decreases significantly.
Atmospheric Pressure vs Elevation
| Elevation (ft) | P_atm (psia) | % of Sea Level | Typical Location |
|---|---|---|---|
| 0 | 14.696 | 100.0% | Sea level |
| 1,000 | 14.173 | 96.4% | Houston, TX |
| 3,000 | 13.171 | 89.6% | Calgary, AB |
| 5,000 | 12.228 | 83.2% | Denver, CO |
| 7,000 | 11.340 | 77.2% | — |
| 10,000 | 10.107 | 68.8% | Mountain passes |
6. Practical Applications
Use in Flow Equations
Average pressure is used to calculate gas properties (Z, ρ, μ) in flow equations like Weymouth, Panhandle A/B, and the General Flow Equation.
Common Errors to Avoid
| Error | Impact | Correction |
|---|---|---|
| Using arithmetic mean for large ΔP | Underestimates P_avg by 2-6% | Use two-thirds when ΔP > 10% |
| Using gauge instead of absolute | ~2% error at low pressures | P_abs = P_gauge + P_atm |
| Ignoring elevation for P_atm | ~2.5 psi error at 5000 ft | Calculate P_atm from elevation |
Industry Standards Reference
| Standard | Application |
|---|---|
| GPSA | Two-thirds formula for gas flow |
| AGA Report No. 3 | Orifice metering calculations |
| Crane TP-410 | Fluid flow reference |
| US Std Atmosphere 1976 | Atmospheric pressure model |
Ready to use the calculator?
→ Launch Calculator