Multiphase Pipeline

Beggs-Brill Correlation

Predict two-phase pressure drop and liquid holdup across any inclination with a defensible, field-ready workflow.

Launch calculator Know the limits

Angle coverage

-90° to +90°

Handles horizontal, uphill, and downhill runs.

Error band

±20–30% ΔP

Plan sensitivities; validate with field data.

Flow map

4 regimes

Segregated, intermittent, distributed, transition.

Contents

Use this correlation when you need to:

  • Screen two-phase pressure drop in gathering lines.
  • Estimate slugging risk on hilly terrain.
  • Bound compressor suction pressure with multiphase flow.

1. Correlation Overview

The Beggs-Brill (1973) correlation predicts pressure drop and liquid holdup for two-phase gas-liquid flow in pipes at any inclination angle. It remains widely used for gathering systems and pipelines.

Key Features

Inclination

-90° to +90°

Robust for downhill liquid draining and uphill accumulation scenarios.

Regimes

4 patterns

Segregated, intermittent, distributed, transition via λL and NFR.

Holdup

Inclination-corrected

Starts with horizontal holdup, then applies ψ(θ) factor.

Friction

2Φ multiplier

Single-phase Moody factor with S-based multiplier for slip.

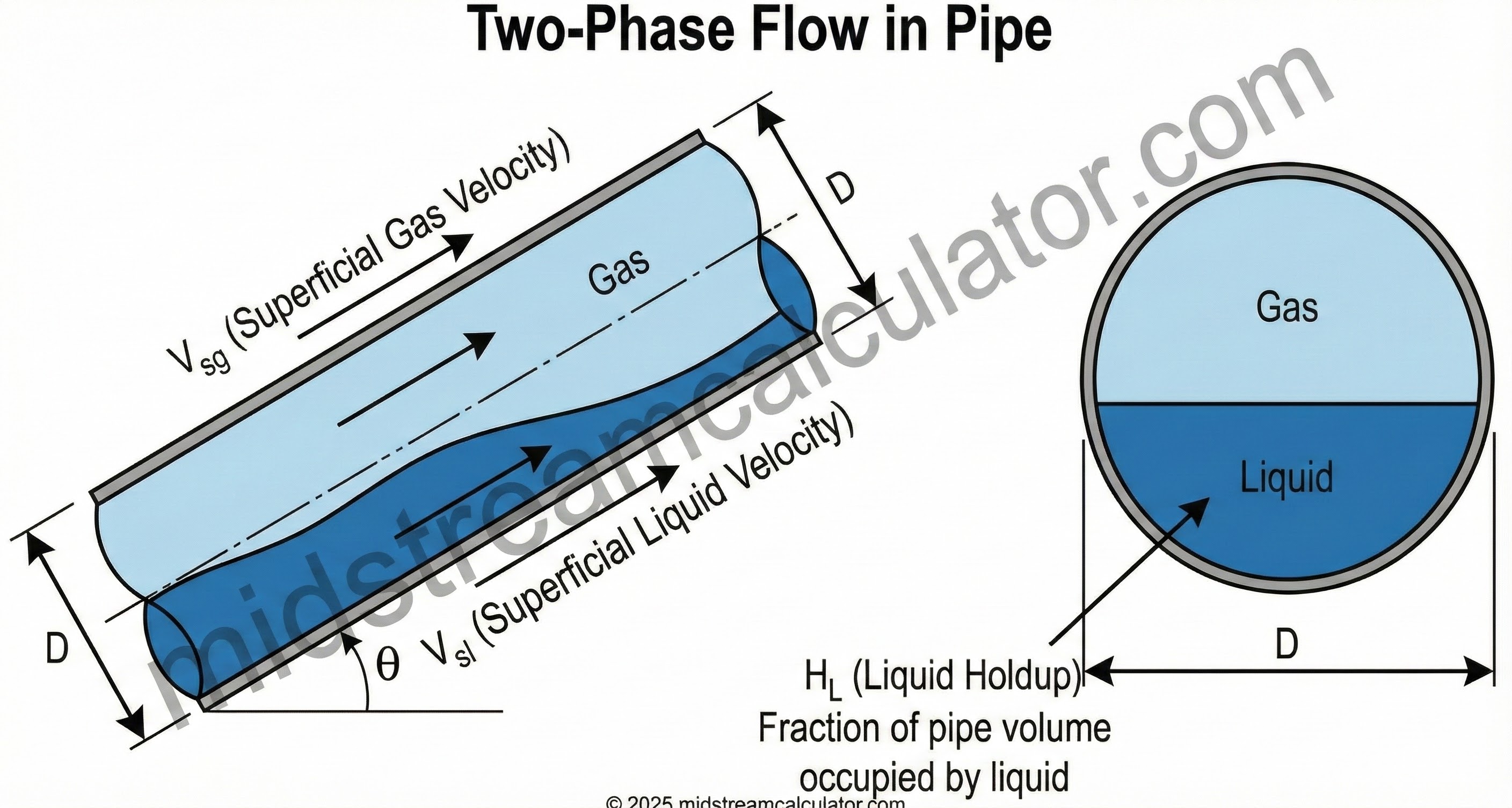
Two-phase gas liquid flow diagram showing superficial velocities, holdup, diameter, and inclination angle.
Two-phase flow schematic with superficial velocities (V_sg, V_sl), liquid holdup H_L, pipe diameter D, and inclination angle θ.

Input Parameters

Parameter Symbol Units
Superficial gas velocity V_sg ft/s
Superficial liquid velocity V_sl ft/s
Pipe inside diameter D ft
Inclination angle θ degrees
Gas density ρ_g lb/ft³
Liquid density ρ_l lb/ft³
Gas viscosity μ_g cp
Liquid viscosity μ_l cp
Surface tension σ dyne/cm

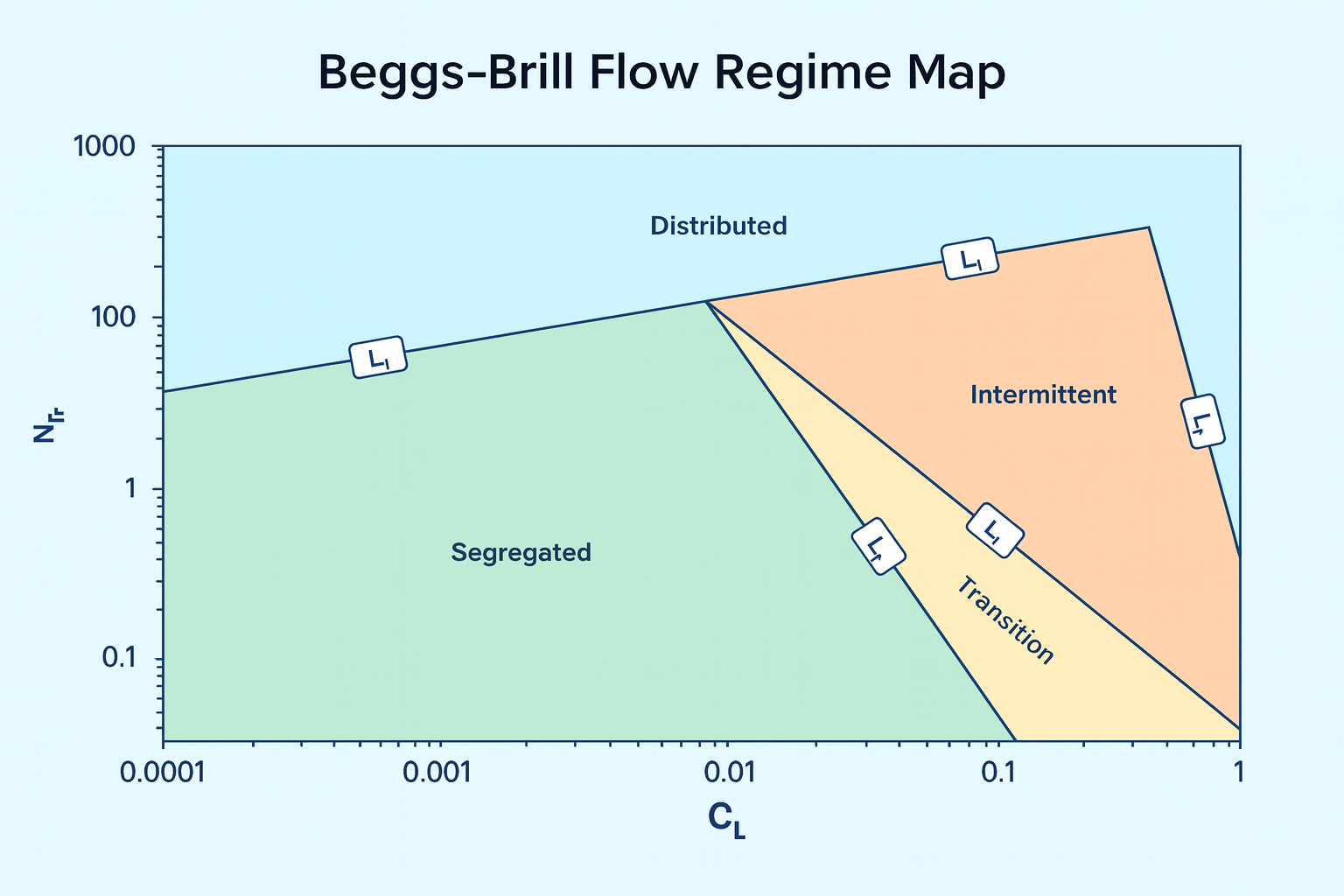
2. Flow Regime Determination

Beggs-Brill identifies four flow patterns based on dimensionless parameters:

Dimensionless Parameters: λ_L = V_sl / V_m (Input liquid fraction, no-slip) V_m = V_sg + V_sl (Mixture velocity) N_FR = V_m² / (g × D) (Froude number) Transition Boundaries: L1 = 316 × λ_L^0.302 L2 = 0.0009252 × λ_L^(-2.4684) L3 = 0.10 × λ_L^(-1.4516) L4 = 0.5 × λ_L^(-6.738)
01

Calculate λL and NFR. Use superficial velocities and diameter; keep units consistent.

02

Pick the regime. Compare NFR to L1–L4; flag if λL is outside test range.

03

Select coefficients. Regime drives holdup constants and inclination correction factors.

Flow Regime Map

Regime Condition Description
Segregated λ_L < 0.01 and N_FR < L1
or λ_L ≥ 0.01 and N_FR < L2		 Stratified or annular; phases separated
Intermittent 0.01 ≤ λ_L < 0.4 and L3 < N_FR ≤ L1
or λ_L ≥ 0.4 and L3 < N_FR ≤ L4		 Slug or plug flow; alternating phases
Distributed λ_L < 0.4 and N_FR ≥ L1
or λ_L ≥ 0.4 and N_FR > L4		 Bubble or mist; phases well-mixed
Transition L2 < N_FR < L3 Between segregated and intermittent
Beggs and Brill flow regime map with lambda L on the x-axis and Froude number on the y-axis showing segregated, intermittent, distributed, and transition regions.
Beggs-Brill flow regime map (λ_L vs N_FR) with boundaries L1–L4 and regime zones.

3. Liquid Holdup

Liquid holdup (H_L) is the fraction of pipe volume occupied by liquid. Beggs-Brill calculates horizontal holdup first, then corrects for inclination.

Horizontal Holdup (H_L(0))

H_L(0) = a × λ_L^b / N_FR^c Coefficients by regime: Segregated: a = 0.980, b = 0.4846, c = 0.0868 Intermittent: a = 0.845, b = 0.5351, c = 0.0173 Distributed: a = 1.065, b = 0.5824, c = 0.0609 Constraint: H_L(0) ≥ λ_L (holdup cannot be less than input fraction)

Inclination Correction

H_L(θ) = H_L(0) × ψ Correction factor ψ: ψ = 1 + C × [sin(1.8θ) - 0.333 × sin³(1.8θ)] Where C depends on flow direction: Uphill (θ > 0): C = (1 - λ_L) × ln(d × λ_L^e × N_LV^f × N_FR^g) Downhill (θ < 0): C = (1 - λ_L) × ln(d' × λ_L^e' × N_LV^f' × N_FR^g') N_LV = V_sl × (ρ_l / (g × σ))^0.25 (Liquid velocity number)

Inclination Coefficients

Regime d e f g
Segregated uphill 0.011 -3.768 3.539 -1.614
Intermittent uphill 2.96 0.305 -0.4473 0.0978
Distributed uphill No correction (C = 0)
All regimes downhill 4.70 -0.3692 0.1244 -0.5056
Physical meaning: Holdup increases on uphill flow (liquid accumulates) and decreases on downhill flow (liquid drains faster). Slug flow in hilly terrain can cause severe holdup variations and slugging at downstream facilities.

Test basis

1–1.5" pipe

Expect larger error on big trunklines; compare with OLGA/field data.

Viscosity range

Light/medium

Accuracy falls for high-visc oils; watch μ_l > ~30 cp.

GVF comfort zone

20–95%

Extremes (near 0% or 100% liquid) behave closer to single-phase limits.

4. Pressure Drop Calculation

Total pressure gradient has three components:

(dP/dL)_total = (dP/dL)_friction + (dP/dL)_elevation + (dP/dL)_acceleration For most pipelines, acceleration term is negligible: (dP/dL)_total ≈ (dP/dL)_f + (dP/dL)_el

Elevation Component

(dP/dL)_el = ρ_m × g × sin(θ) / 144 ρ_m = ρ_l × H_L + ρ_g × (1 - H_L) (Mixture density) Where: dP/dL = psi/ft ρ = lb/ft³ g = 32.174 ft/s²

Friction Component

(dP/dL)_f = f_tp × ρ_n × V_m² / (2 × g × D × 144) ρ_n = ρ_l × λ_L + ρ_g × (1 - λ_L) (No-slip density) Two-phase friction factor: f_tp = f_n × e^S f_n = Moody friction factor at Re_n = ρ_n × V_m × D / μ_n μ_n = μ_l × λ_L + μ_g × (1 - λ_L) S parameter: y = λ_L / H_L² If 1 < y < 1.2: S = ln(2.2y - 1.2) Otherwise: S = ln(y) / (-0.0523 + 3.182×ln(y) - 0.8725×(ln(y))² + 0.01853×(ln(y))⁴)

Example Calculation

Given: 6" pipe, 5° uphill, V_sg = 10 ft/s, V_sl = 2 ft/s, ρ_g = 3 lb/ft³, ρ_l = 50 lb/ft³

V_m = 10 + 2 = 12 ft/s λ_L = 2/12 = 0.167 N_FR = 12²/(32.2 × 0.5) = 8.9 → Intermittent flow regime H_L(0) = 0.845 × 0.167^0.5351 / 8.9^0.0173 = 0.35 Inclination correction → H_L ≈ 0.42 ρ_m = 50×0.42 + 3×0.58 = 22.7 lb/ft³ (dP/dL)_el = 22.7 × 32.2 × sin(5°) / 144 = 0.044 psi/ft
Check

Bound with single-phase. Compare ΔP to gas-only and liquid-only to sanity check output.

Sensitivity

Vary λL and angle. Small changes in input fraction or inclination can swing holdup significantly.

Validate

Cross-check in field. Match against pressure survey or smart pig data where available.

5. Limitations & Alternatives

Beggs-Brill Limitations

Alternative Correlations

Correlation Best Application
OLGA / LEDAFLOW Dynamic multiphase simulation, severe slugging
Mukherjee-Brill Oil wells, deviated wells
Duns-Ros Vertical gas wells
Hagedorn-Brown Vertical oil wells
Gray Wet gas vertical flow
Oliemans Large diameter, high pressure gas-condensate

Use confidently

Light oil / gas, modest diameters

Gathering lines, early feasibility, incline-aware screening.

Use with caution

High slug risk or steep slopes

Expect larger holdup swings; consider dynamic modeling.

Avoid

Heavy crude or 3-phase

Use mechanistic/OLGA or field-calibrated models instead.

⚠ Validation required: Always compare correlation predictions against field data when available. Multiphase correlations can have significant errors—use multiple methods and engineering judgment.

References

Ready to calculate?

→ Beggs-Brill Calculator

Related Calculators