Hydraulic Design

Pipe Fitting K-Factors

Calculate pressure drop across fittings and valves using Crane TP-410, Hooper 2-K, or Darby 3-K methods.

Launch calculator Compare methods

Crane TP-410

K = (L/D) × f

Industry standard. Turbulent flow.

Hooper 2-K

Re correction

Better for transitional flow.

Darby 3-K

Most accurate

Re + size scaling. All regimes.

Contents

Use this guide to:

  • Calculate fitting pressure drop.
  • Select method for your flow regime.
  • Look up K-factors and coefficients.

1. K-Factor Basics

The loss coefficient (K) relates pressure drop to velocity head. Higher K = more pressure loss for the same flow.

Pressure Drop: ΔP = K × ρV² / (2g × 144) [psi] Velocity Head: hᵥ = V² / 2g [ft] Equivalent Length: Leq = K × D / f [ft] Where: K = loss coefficient, ρ = density (lb/ft³), V = velocity (ft/s), g = 32.174 ft/s², D = diameter (ft), f = friction factor
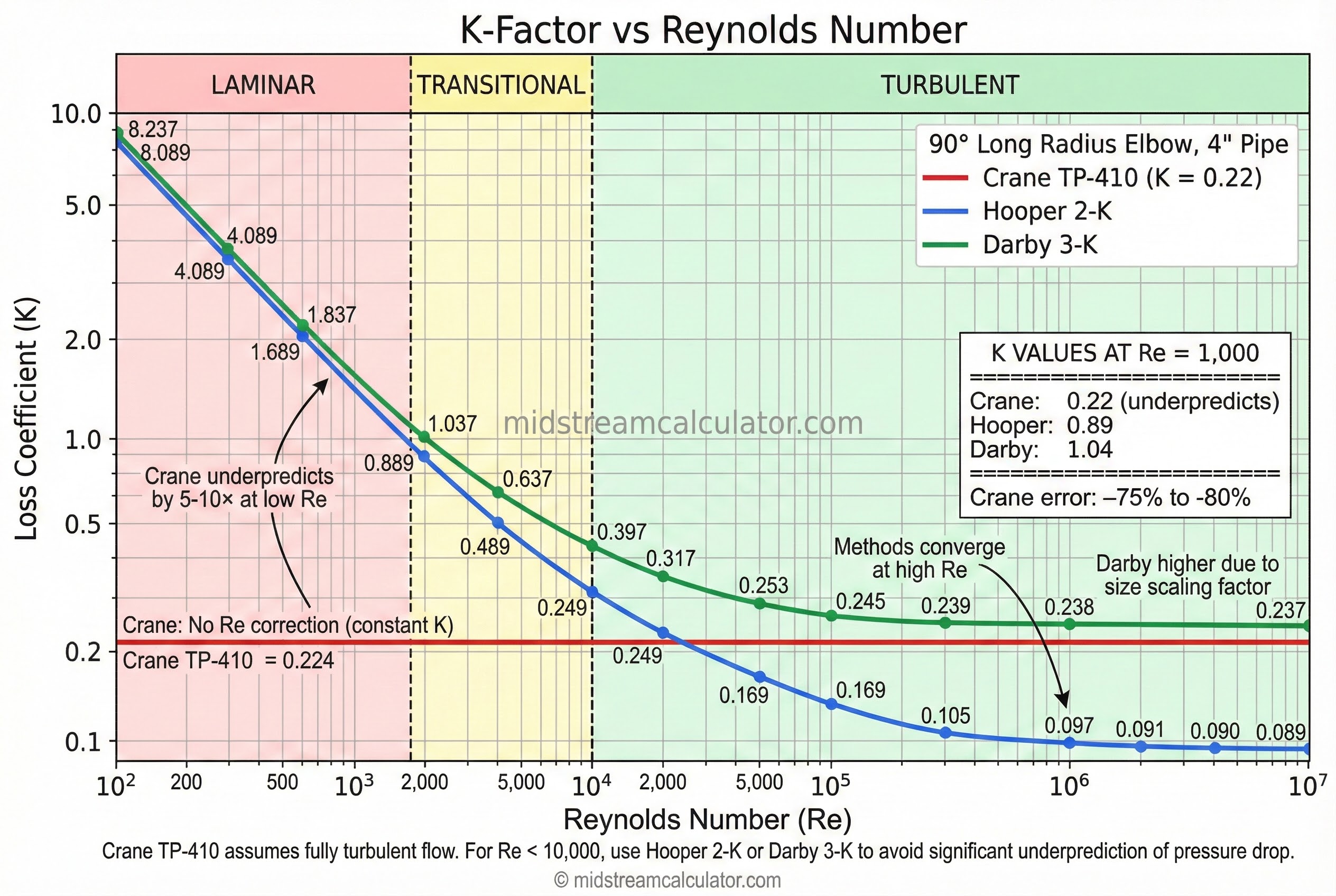
K-factor versus Reynolds number comparing Crane, Hooper 2-K, and Darby 3-K methods.
K-factor vs Reynolds number for a 90° elbow using Crane, Hooper 2-K, and Darby 3-K methods.

Flow Regime Effect

Laminar (Re < 2,100)

K ∝ 1/Re

K increases sharply. Use Darby 3-K.

Transitional (2,100-10,000)

Variable

Unstable. Hooper or Darby.

Turbulent (Re > 10,000)

K ≈ constant

Crane adequate.

2. Method Comparison

Method Equation Best For Accuracy
Crane TP-410 K = (L/D) × fT Turbulent (Re > 10,000) ±15%
Hooper 2-K K = K₁/Re + K∞(1 + 1/D) All regimes, moderate accuracy ±10%
Darby 3-K K = Km/Re + Ki(1 + Kd/D0.3) All regimes + size scaling ±5%

Equation Details

Crane TP-410: K = (L/D) × fT Where: L/D = equivalent length ratio (from tables) fT = friction factor at full turbulence Hooper 2-K: K = K₁/Re + K∞(1 + 1/Dᵢₙ) Where: K₁ = laminar coefficient K∞ = turbulent coefficient Dᵢₙ = pipe ID in inches Darby 3-K: K = Km/Re + Ki(1 + Kd/Dnom^0.3) Where: Km = laminar coefficient Ki = turbulent coefficient Kd = size scaling factor Dnom = nominal pipe size (inches)

Example: 90° LR Elbow, 4" Pipe

Re Crane Hooper 2-K Darby 3-K
1,000 (laminar) 0.22 0.89 0.97
5,000 (transitional) 0.22 0.25 0.30
50,000 (turbulent) 0.22 0.16 0.25
500,000 (fully turbulent) 0.22 0.16 0.24

Note: Crane significantly underpredicts at Re = 1,000. All methods converge at high Re.

3. K-Factor Tables

Crane L/D Values and Turbulent K

Fitting L/D K (f=0.016)
90° Standard Elbow 30 0.48
90° Long Radius Elbow 14 0.22
45° Elbow 16 0.26
Tee - Flow Through Run 20 0.32
Tee - Flow Through Branch 60 0.96
Gate Valve (open) 8 0.13
Globe Valve (open) 340 5.44
Ball Valve (full bore) 3 0.05
Check Valve (swing) 100 1.60
Butterfly Valve (open) 45 0.72

Hooper 2-K Coefficients

Fitting K₁ K∞
90° Std Elbow (welded) 800 0.091
90° Std Elbow (threaded) 800 0.140
90° Long Radius Elbow 800 0.071
45° Elbow 500 0.071
Tee - Run (threaded) 200 0.091
Tee - Branch (threaded) 500 0.274
Gate Valve (open) 300 0.037
Globe Valve (open) 1500 1.700
Ball Valve (full bore) 300 0.017
Butterfly Valve 1000 0.690

Darby 3-K Coefficients

Fitting Km Ki Kd
90° Std Elbow (welded) 800 0.091 4.0
90° Std Elbow (threaded) 800 0.140 4.0
90° Long Radius Elbow 800 0.071 4.2
45° Elbow 500 0.071 4.2
Tee - Run 200 0.091 4.0
Tee - Branch 500 0.274 4.0
Gate Valve (open) 300 0.037 3.9
Globe Valve (open) 1500 1.700 3.6
Ball Valve (full bore) 300 0.017 3.5
Butterfly Valve 1000 0.690 4.9

Crane Friction Factor (fT) by Pipe Size

Nominal Size ½" 1" 2" 4" 6" 8" 12" 16"+
fT 0.027 0.023 0.019 0.016 0.015 0.014 0.013 0.012

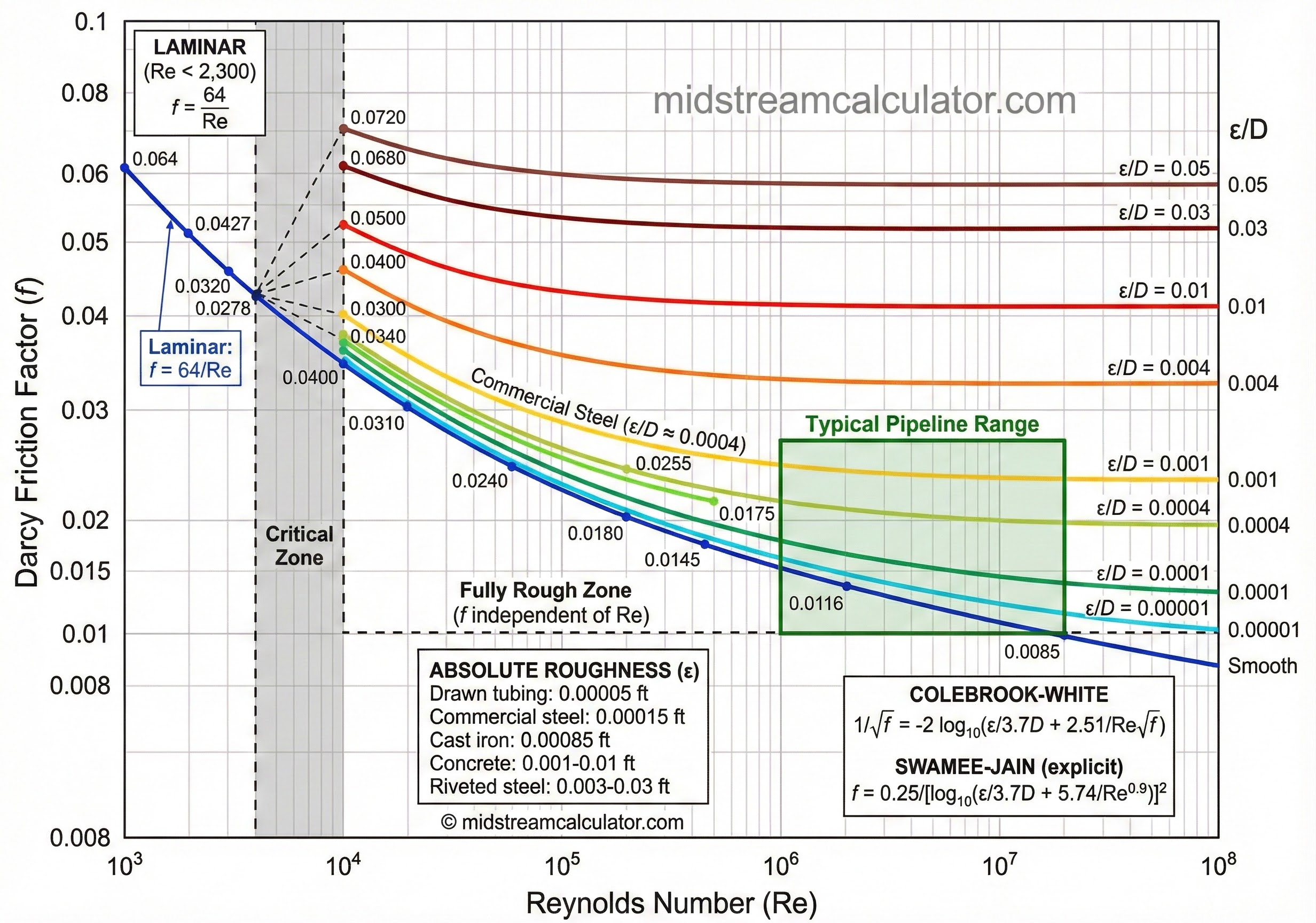
4. Straight Pipe Friction

For pipe sections, K = f × L/D where f comes from Colebrook-White or Moody diagram.

Laminar (Re < 2,100): f = 64/Re Turbulent (Swamee-Jain, explicit): f = 0.25 / [log₁₀(ε/3.7D + 5.74/Re^0.9)]² Turbulent (Colebrook-White, implicit): 1/√f = -2 log₁₀(ε/3.7D + 2.51/Re√f) Valid: 5,000 < Re < 10⁸, 10⁻⁶ < ε/D < 0.01

Pipe Roughness (ε)

Material ε (ft) ε (mm)
Commercial Steel (new) 0.00015 0.046
Commercial Steel (corroded) 0.0007 0.21
Stainless Steel 0.00005 0.015
PVC / HDPE 0.000005 0.0015
Concrete 0.001-0.01 0.3-3.0
Cast Iron 0.00085 0.26
Moody diagram showing Reynolds number versus Darcy friction factor with roughness curves.
Moody diagram: friction factor vs Reynolds number with relative roughness curves and typical pipeline operating range.

5. Method Selection

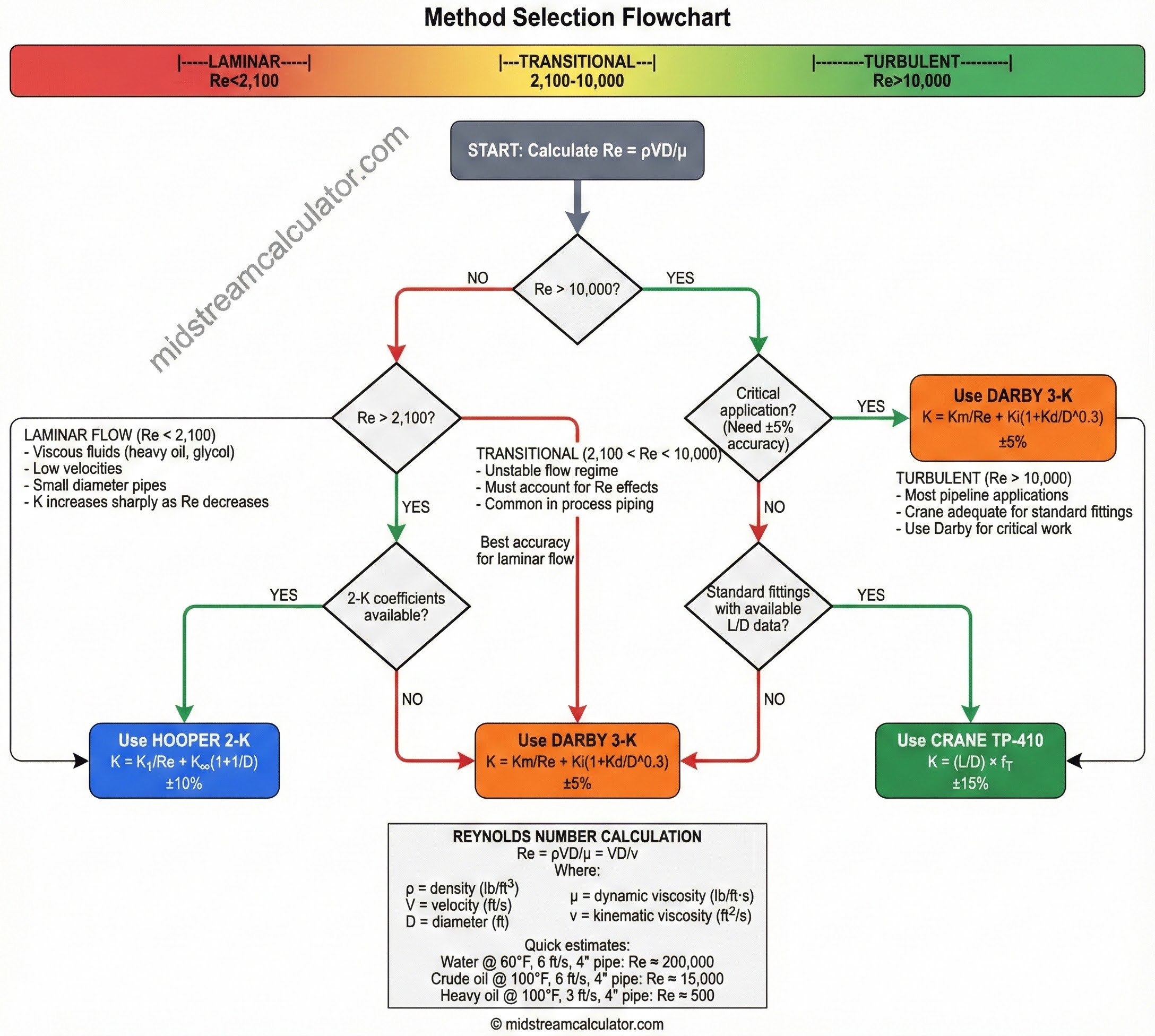
Flowchart selecting Crane, Hooper 2-K, or Darby 3-K based on Reynolds number and application.
Method selection flowchart: choose Crane for turbulent standard fittings, Hooper for transitional, Darby for laminar/specialty or high accuracy.

Quick Selection Guide

Condition Method Why
Re > 10,000, standard fittings Crane Simple, widely accepted
2,100 < Re < 10,000 Hooper or Darby Re correction needed
Re < 2,100 (laminar) Darby 3-K Best laminar accuracy
Large pipe (>12") or small (<2") Darby 3-K Size scaling improves accuracy
Critical hydraulic design Darby 3-K Highest accuracy (±5%)
Preliminary estimates Crane Quick, conservative

Common Mistakes

References

Ready to calculate?

→ Fitting K-Factor Calculator

Related Calculators